てれじょんのメモ帳

twitter(@television_met)に書ききれないことを投稿します。

Kelvin-Helmholtz不安定の(単純な)数値実験例

おはこんばんにちはてれじょんです。

今年こそ記事を色々書きたいと宣言した年末から早くも3ヶ月ちょっとが過ぎてしまいました。皆様いかがお過ごしでしょうか。

私の方はM1になったり、地球連続体力学のTAになったりと、まあ色々やっています。あと最近はお絵描きの練習をしてたりします。一応毎日何かしら書くのを目標にしており、misskeyに模写を投稿したりしてます。たまに行くバーで会った作家さんの勧めで、モルフォ人体デッサンの「箱と円柱で書く」ってやつをやっています。何かおすすめがあれば教えてくれれば嬉しいです。


サムネ用の図です。


さて、前置きが長くなりましたが本題です。

いままで色々数値実験をしてきたのですが、実験設定とかをまとめていなかったため、謎の設定でされた計算の結果がサーバーに溜まっている状況になってしまいました。

色々と不便なので、やったそばからブログに残すことにしました。*1今回はKelvin-Helmholtz不安定(以下KH不安定)です。



支配方程式は以下の渦度方程式です。

\displaystyle\frac{D\zeta}{Dt}=-\nu\nabla^8\zeta

普通のKH不安定であれば圧縮性もあり、密度成層するような状況を考えるわけですが、ここでは単純な例ということで非圧縮で密度一定の流体を考えています。したがって、バロトロピックな不安定性だけが見られるという設定になっています。また、後述の通りスペクトル法で計算を行ったので、計算の安定のために高階粘性を導入しています。

さて、非圧縮流体なので流線関数\psiを導入することができます。

\displaystyle u=-\frac{\partial\psi}{\partial y},~~v=\frac{\partial \psi}{\partial x}

この流線関数を以下のように関数展開してスペクトル法で計算を行いました。
スペクトル法を用いるため、領域はx-yの二次元とし、両方向に周期境界条件を課しています。
\displaystyle \psi(x,y)=\sum_{n=-N}^N\sum_{m=-M}^M\hat{s}_{n,m}\exp\left(\frac{2\pi inx}{L_x}\right)\exp\left(\frac{2\pi imy}{L_y}\right)

その他の実験設定は以下のようになっています。

水平・垂直切断波数N,M 170
水平・垂直格子点数J,K 512
領域の水平長さL_x 4
領域の垂直長さL_y 2
高階粘性係数\nu 2.0\times 10^{-18}
時間発展 4段4位Runge-Kutta (線型項は分離)
時間刻み幅 1/50 or 1/100

初期条件には以下のような速度場を用意しました。この速度場になるような流線関数を求め、そこに振幅が1.0\times10^{-15}の乱数をすべての波数に与えました。このように摂動を与えると、発達速度の一番大きな不安定モードが発達し、その波数の波が卓越する様子を観察できます。
\displaystyle u(x,y,0)=A\tanh\left(B\cos\pi y\right),~~~~v(x,y,0)=0

初期の速度場
<>
初期の渦度場

さて、実験結果は以下のようになりました。まずはA=1/3,~~B=3の結果です。
youtu.be

t=40くらいから不安定になり、波数3の構造が発達している様子が見えます。
また不安定が十分発達したあと、各々の渦は切離して孤立渦になっています。この孤立渦が相互作用して、乱流状態へと移行する様子も観察できます。

次はA=1/5,~~B=5の結果です。

youtu.be

こちらもt=40くらいから不安定になっていますが、今度は波数5の構造が発達しています。
見える構造が変わった理由ですが、これはシアー層の幅が小さくなったことに起因しています。
詳しくは各自調べてほしい*2のですが、線型安定性解析より、波長の短い波ほど発達率が大きいことがわかります。ただ、波長が短すぎると粘性の効果で散逸されやすくなったり、そもそも空間スケールが小さいためかき混ぜるスケールも小さいなどの理由から、ある程度の長さを持つ波長の波が発達することになります。ところで同じく線型安定性解析より、摂動はシアーの境界からの距離に対して指数関数的に(e^{-ky}のオーダーで)減衰することがわかります。そのため、シアー層の部分が厚くなると、波長の短い波はより減衰しやすくなり、最も発達率の大きな波の波長は更に長くなります。

以上です。今年度はB4もM1もたくさんいるため、こういうふうにゼミにかこつけて数値計算する機会が少なくなってしまうかも知れませんが、まあ何かしら記事に残したいです。最後にした説明はだいぶ大雑把なので、いい説明がある人はぜひコメントとかしてください。閲覧ありがとうございました。

*1:てか最初の方からそうやって使ってたじゃん。サボってただけ……

*2:Atmospheric and Oceanic Fluid DynamicsのChapter9前半とか

2022年の出来事

おはこんばんにちはてれじょんです。

 

来年こそはちゃんとブログに記事を残したい！！！！！

 

ツイッターで適当に細切れの文章を放流するよりは、まとまった量の文章を真面目に(?)書いたほうが良いような気がしてきたというのが一つあります。というのも、自分の考えていることを筋道立てて他人に説明する、というのは結構訓練の必要な行為で、そのスキルが不足しているのを痛感したのが2022年だったからです。研究活動*1のプレゼンや論文書きはもちろん、研究活動2*2の感想を他人に伝えたい時等困らないよう、訓練を重ねていきたいものです。(適当にブログ書いてるだけで身につくんかいという話もありますが)

その第一歩として、今年(2022年)の振り返り記事を書きます。

研究室配属

4回生になり、課題研究をするにあたって研究室配属がありました。今年の地物は流体系の研究室の人気が高く、研究室以前にそもそもT2に通るかが不安で日々ビクビクしていましたが、無事T2に通り、(形而上)気象学研究室に配属になりました。

大気モデルを自分で組みたいと前々から思っていた旨を教授に伝えたところ、面白そうなテーマを設定してくれたので、それに向けて研究活動を開始しました。

図1. 形而上気象学研究室のイメージ図

研究進捗ですが、多分結構いい感じの結果が出ています。ただ、2022/12/30 18:06現在卒論の執筆を何もしていないのでそろそろまずいんじゃないかという気持ちになってきました。別に良くね？卒論とか書かなくても*3

卒論のモチベは特にありませんが、投稿論文にはまとめたいという気持ちがあります。フルペーパーになるかはわかりませんが、M1のうちに一本出してやりたいです。みてろよ。

大学院入試

二度とやりたくないです。

京都大学大学院 理学研究科の地球惑星科学専攻と、東京大学大学院 理学系研究科の地球惑星科学専攻の両方を受けて両方受かりました。やった〜。そもそもなんで2つ受けたのかという話ですが、もともと極地の研究に興味があってというかぶっちゃけ南極に行きたいってそれだけなんですけど、それを精力的にやっている東大の研究室に行きたいと思っていたんですよね。なので今やってるライブラリ開発やモデル構築は東大で趣味的にやっていこうと漠然と考えていたわけですが、卒業研究でGCMを実装していく中、数値計算法をもっと勉強したいという気持ちになってきました。悩みに悩みに悩みに悩みに悩みに悩みに悩んだ結果、僭越ながら東大は辞退して京大の方に引き続きお世話になることにしました。

正直南極に未練が無いかと言われるとまあ嘘になるんですが、やると決めた以上この道で頑張っていきたいです。頑張ります。

図2. なんか京大の方は首席合格でした。ウケる。
東大の方は340点くらいでしたが、他の人がどうなのか知らないので良いのか悪いのかわかりません。

それはそうとして、大学院入試は二度とやりたくないです。

ちくわサラダ演習

またの名を観測地球物理学演習Aといいます。2回生配当の演習ですが、私が2回生、3回生の時は連続で不開講になりました。名前を言ってはいけない例のウイルスのせいです。今年こそ開講されたため、4回生なのに無理言って履修させてもらえました。担当された先生方には本当に頭が上がりません。

肝心の内容ですが、

・地球電磁気

・気象観測

・重力観測

の3つのことをやりました。順に説明します。

まず地球電磁気ですが、アルミパイプ等を使ってアンテナを自作し、それを使って流星の電波を受信する、ということをしました。正確には、電波は地上から宇宙に向かって送信されていて、その電波が流星によって反射されて地上にやってくるため、反射波を観測することで間接的に流星を観測する、ということをしました。

次に気象観測ですが、地上からバルーンを打ち上げて、そのバルーンの方位角と仰角をつかって上空の風を観測しました。バルーンの位置情報は空間3次元で特定できるけど、わかるのは方位角と仰角だけなので、上昇速度を仮定して30秒ごとに観測することで、高度を無理やり仮定しました。経緯儀を2つ使って観測したので、両方の経緯儀の情報を使えば更に精度良く推定できるのですが、めんどくさかった時間がなかったのでやりませんでした。それでも98点とかgetできたので、レポートの体裁がしっかりしてれば何でも良いんだと思います。

最後の重力観測です。これは泊まっていた宿舎の各階で重力計を使って重力を観測して、重力の値が高度に依存してどう変化するか、ということをしました。全く同じ内容のことを3回生の課題演習でやっていたので内容は全部知っていましたが、実際やってみると理論値からかなり離れているのが面白かったです。まあその理由も課題演習で全部ネタバレされてましたが。横軸高度で縦軸相対重力の変分、というグラフを書いたのですが、回帰直線の決定係数が(丸められて)1.0になってびびった記憶があります。

図3. ちくわサラダ　年始にちくわサラダパーティーします

データ同化の勉強

前期にデータ同化Aが開講されていたので、なんとなく履修しました。理研のバケモノ天才研究者であるところのmys先生とootk先生にシバかれる可愛がってもらえるとても楽しい講義です。半期通して扱う課題の一覧が最初の講義で与えられて、3人くらいのグループを作って一緒に課題に取り組むスタイルでした。毎回最初に5分くらい進捗報告をしなければならない上、課題もまあまあ重いので講義が多い人にはあまりおすすめできません。でもデータ同化筋*4は確実に鍛えられます。私は右も左もわからない状況からスタートしましたが、最終的にはアンサンブルカルマンフィルタとかが実装できるようになりました。LETKFとかも実装できるようになるので、計算パワーさえあれば大自由度系に適用することもできます。

講義での縁もあり、夏休みは理化学研究所のインターンシッププログラムに参加してきました。2週間〜1ヶ月の間で期間を希望して、その期間を使って研究チームの人と色々やる、というものです。私は例のデータ同化研究チームに配属になり、1000メンバーのアンサンブル予報の結果解析を行いました。成果が非静力学モデルワークショップで公開されたので、興味が合ったらご覧ください。私は2週間しか居なかったのですが、もっと実習期間があったら色々できたな〜という感じだったので、応募したい方はぜひ長めの期間を希望したほうが良いと思います。

あと後期はデータ同化Bの講義を受講したかったんですが、希望者が僕しか居なくて不開講になりました。涙……　その代わり(?)に、理学部のmacsプロジェクトの一環として、引き続きmys先生とootk先生に教わりながら色々面白いことやろうぜ！みたいなことをしています。現状ですが、手持ちの浅水系のモデルにデータ同化を適用する、ということをしています。LETKFの実装がしんどかったですが、面白そうな結果も出ているので、こっちの方でも何かしら成果を上げたいと思います。その前に今年度の結果発表のプレゼンをしなければならないわけですが……

台湾に行った

国立台湾大学と京都大学の気象系研究室のジョイントワークショップであるところのNTU KU joint workshopに参加してきました。台湾の入国制限が緩和されない限りは行けないね〜という感じだったので正直僕も行けるとは思っていなかったのですが、確か10月の中旬辺りに制限が緩和され、そこからはトントン拍子で物事が進みました。人生初の公式な発表、しかも海外かつオーラルで無茶苦茶緊張しましたが、なんとか無事終わって良かったです*5。

プレゼンの内容は、球面調和関数変換の高速な実装と、卒業研究でやっているドライGCMの実装の概要、あとテストケース(Polvani, et al. 2004)の実行結果についてです。全部ツイッターに垂れ流していた内容だったので、ツイートをまとめたらいい感じになりました。それでええんか？

図4. 実行結果。Polvani, et al. 2004と全く同じ実験設定です。

向こうの学生や先生たちの発表も面白かったです。と同時に、向こうの学生は英語がすごく上手だったので、語学の勉強もちゃんとやらないとなあという気持ちになりました。読み書きはまあまあ得意なんですけどね。話す・聞くがちょっと苦手です。

また、向こうの人たちにはとても親切にしてもらいました。初日と最終日の両方でお土産を頂いたり(???)、ワークショップ後に台湾の街を案内してもらったり、ジオパークに連れて行ってもらったりしました。私のしょーもない質問にも付き合ってもらったりで、感謝してもしきれません。お土産でもらったマグカップは研究室で使っています。本当にありがとう。来年度以降も継続していってほしいものです。

アニメとか

今年は本当に面白いアニメが色々ありましたね〜〜〜〜〜〜〜〜〜（大声）

まちカドまぞく2期のおかげで私は院試を乗り越えられましたし、直前にニジガクの2期を摂取したおかげで首席合格できましたし(要検証)、その後もエンゲージキスとかルミナスウィッチーズとかプリマドールとかDo it yourself!とかぼっち・ざ・ろっくとか本当に見るアニメに欠かない一年でした。スローループも原作を買ってしまうくらいには良かったですし、水星の魔女も今後の展開が気になります。

しかしやはりなんと言っても今年はヤマノススメ Next Summitが最高でした。あんなに自分のことしか考えられず、幼馴染のことすら忘れてしまうような人間だった雪村あおいが成長した姿がこれでもかと言うほど存分に描かれており、とても味わい深かったです。OPのジャングルジムのカットで高所恐怖症を克服した様子が端的に表されている所とか、あおいが歩く道に花が咲くことで次の季節を想起させるところとかといった細部の描写もさることながら、「Next Summit」で「次の頂き」が続いていくことを明示して物語を終わらせてくるという大局的な構成も完璧だと思います。頂きの先の向こうも道は続いていくんだよな……　あとは毎回絵柄が変わるEDが良すぎた……　EDだけなら各話10回は見ました。僕は4話、7話、12話、11話、2話、1話、5話、8話、9話、6話、10話、のEDが好きです。みんなは何話のEDが好き？　大学後半戦以降、こういうジワジワ〜〜と効いてくるタイプのアニメが好きになってきましたね。高校生の頃とかはゆるキャンとか見てもあまり刺さらなかったのですが、最近になって見返したら無茶苦茶良くて涙が止まりませんでした。

図5. このふたりの関係性も好きです……

 

リコリス・リコイルはどうしたんだよ？？？？

面白くなかったみたいなツイートをした記憶があるんですが、あれはちょっと正確ではなくて、結局何を伝えたいのかよくわからなかった、というのが正直な感想なんですよね。千束とたきなの物語として即自的に捉えられているところもありますが、千束は結局たきなの前から逃げて病院を脱走したわけなので、最初から最後までたきなのことをそこまで大事に思っているわけでもなさそうですし、たきなはと言えば依存先がDAから千束になっただけなので、本質的には何も変わってないじゃないですか。千束と真島の対立で見るのが筋のような気もするんですが、どっちが正義とか悪とか言うわけでもないし、それを決めるのは難しい(というかナンセンス)ですよね、というふうに解釈するしか無い気がします。

しかしながらにしてリコリスという社会的弱者を搾取することによって仮初の"幸福な"社会が実現しているという構図はものすごく気持ちが悪いですし、やはりDAが破壊されないことにはハッピーエンドにはなりえないと思うんですよね。でもそれを実現するのは1リコリスには不可能でしょうし、そういうものを踏まえた上での「世界を好みの形に変えている間に、おじいさんになっちゃうぞ」という千束の発言があったんでしょうけど……　この間友人に「てれじょんってリコリコのこと悪く言う割にいつもリコリコのこと話してるよね」と言われました。結局の所リコリコのことは否定しようもなく好きなんでしょうね。嫌いってことは、好きってことなので(百合？)。まあ2期とか今後の展開が何かしらあるでしょうし、そこで全部のワロタが回収されて神になることを期待しています。

来年の抱負

今年は色々新しいことができました。でも日々やることに追われていたため、腰を据えてじっくり考えるということが出来ていなかったようにも感じます。来年度はあまり焦らず、じっくり物事を考えたり、本を読んだりする時間を作りたいです。あと今の卒業研究の内容をちゃんとまとめて、M1のうちに投稿論文を出したいです。フランス語とかイラストとかの勉強もしたいですが、そのへんまで手が回るかは正直わかりません……(やりなさい)

*1:原義研究活動

*2:アニメや、漫画などの鑑賞

*3:卒論を書かなくても卒業研究発表会をすれば卒業できるという噂があるので、その裏技に少し期待しています。

*4:データ同化を使うときに必要になる筋肉

*5:本当のことを言うと、質疑応答で質問が全く理解できなくてその場は適当にごまかしました。すみません。でもその後休憩時間にちゃんと説明しに行ったのでノーカンで許してください。

二次元平面上への球面調和関数の図示

おはこんばんにちは(死語)、てれじょんです。

前回記事を書いてからまたしても久方ぶりのブログ更新ですが、今回も球面調和関数関連の話題です。

Twitterではネストありの並列化処理の話を記事に書きたいとか言ってましたが、よくよく調べたら内部変数をちょろっと弄るだけで実現できることがわかり、ブログにするまでもないな……となった次第です。

本題

で、さっそく本題ですが、今回は自作ライブラリ*1を使用して、球面調和関数を二次元平面で図示しました。

御託はあとにして、結果がこちらです。0\leq m\leq 10,~m\leq n \leq10の実部と虚部を図示しました。
mが負の成分については、正の成分の複素共役を取れば良いです。(今の定義では。詳しくは後述。)

コンターインターバルは0.4です。
グリッド数は256(緯度)*512(経度)で計算し、図示にはDCLを使用しました。
数がバカ多くなるので0\leq m\leq 10,~m\leq n \leq10のみに限定して描画していますが、もし需要があったらもっとデカい成分も放流する用意があります*2。

定義

ここで、球面調和関数Y_n^m(\lambda,\mu)は次のように定義しています。
Y_n^m(\lambda,\mu)=P_n^m(\mu)e^{im\lambda}
P_n^m(\mu)=\sqrt{(2n+1)\frac{(n-|m|)!}{(n+|m|)!}}\frac{1}{2^n n!}(1-\mu)^{|m|/2}\frac{d^{n+|m|}}{d\mu^{n+|m|}}\left( (\mu^2-1)^n\right)
ただし\lambdaは経度、\mu=\sin\phiはサイン緯度、\phiは緯度で、P_n^m(\mu)はLegendre陪関数です。
このように定義した球面調和関数には、
\int_{-1}^1d\mu\int_0^{2\pi}d\lambda ~Y_n^m(Y_{n'}^{m'})^*=4\pi \delta_{n,n'}\delta_{m,m'}
という直交関係と
Y_n^{-m}=(Y_n^{m})^*
という偶奇性があります。物理畑の人の定義とは(往々にして)定数倍違うことに気をつけて下さい*3。

で、どういうふうに計算したか？

次のような球面調和関数展開を考えてみましょう。
g(\lambda,\mu)=\sum_{n=0}^M\sum_{m=-n}^n s_n^mY_n^m(\lambda,\mu)
このスペクトルs_n^mを
s_{n'}^{m'}=s_{n'}^{-m'}=1/2
s_n^m=0 (\mbox{otherwise})
と定義すれば、
g(\lambda,\mu)=\left(Y_n^m+\left\{Y_n^{m}\right\}^*\right)/2=\Re(Y_n^m)
となります。したがって、以上の様にスペクトルを定義して、逆変換すれば球面調和関数の値がグリッドスペースでわかります。
虚部についても同様に、
s_{n'}^{m'}=1/2i
s_{n'}^{-m'}=-1/2i
s_n^m=0 (\mbox{otherwise})
と定義すれば
g(\lambda,\mu)=\left(Y_n^m-\left\{Y_n^{m}\right\}^*\right)/2i=\Im(Y_n^m)
で、虚部が求まります。m=0成分はs_{n'}^{0}=1と定義して下さい。
そんな事言われなくても分かってるよ

量子力学の教科書に書いてあるような、3次元の図示はちょっと調べればたくさん出てくるんですが、二次元平面に書いた図って中々なくないですか？
少なくとも私は見つけられませんでした。量子力学エアプなんで詳しくは知りませんが、波動関数の(角度方向の？)の形がどうなってるかとかでイメージしやすいからということで3次元で書く流儀が多いんだと思います。気象学とか、球面上で関数を展開したいというモチベーションを持った人には3次元のプロットよりは2次元のプロットのほうが使いやすい気がするんですけどね。フーリエ変換の時みたいに、どういう形の関数の重ね合わせをすれば表現できるかが直感的にイメージできるので。

以上です。ブログは暇なときにぼちぼち更新したいです。てかTwitterやってる時間あったらブログ書けよ。

サムネイル用の画像です。地球流体電脳倶楽部最高！一番好きな倶楽部です！

*1:前回の記事から紆余曲折あって、卒業研究とかでも使えるまあまあ実用的な計算速度のライブラリができました。これの話もおいおい記事にしたいけど(それはお前がやるんだよ)

*2:T30ですら450枚くらいになっちゃうし、これで十分だと思いますがね……

*3:こう定義したほうが積分領域の面積と一致して気持ちいい気がするんですけどね 他の人のお気持ちがよくわかりません 追記：よく考えたらこれって確率密度の全空間積分が1になるように正規化したいから定数倍ずれるんですね　当たり前じゃん

球面調和関数変換を実装した話

これはなに

　こんにちは、てれじょんです。ブログを書くのは久しぶりですね。最後に記事を書いてからというもの、FFTとか、FSTとかFCTとかまあ色々実装してはいた*1のですが記事を書くのが面倒(しかも別に書かなくてもググればだいたい情報が出てくるし、適当な教科書を読めば大丈夫)で、記事を書いていないのがかれこれ2年くらい続いていました(怠惰の言い訳か？)。しかし最近球面調和関数変換(以下SHT*2 )の実装をしたのですが、ググってもググっても自分で実装しましたみたいな話が全くなくて*3、不便だったので、自分が実装したまでの道筋を備忘録的に残しておこうと思って記事を書くことにしました。自分で実装してないライブラリを使いたくないというモノ好きの人はぜひ読んで下さい。あと何かいい記事を知っている人がいたら教えてください。

　記事の内容ですが、大半が石岡圭一『スペクトル法による数値計算入門』(東大出版会)に依っています。実装に最低限必要なことや、実装の時によくわからなかったことをメインで説明して、ググれば出てくるような数式とかの展開は端折っていこうと思っていますが、コレヤバいだろとか、もっとこういう説明のほうがわかりやすいだろってところがあったら教えてくれると嬉しいです。

SHT is 何

　球面上の関数g(\lambda,\mu)を球面調和関数Y_n^mで

g(\lambda,\mu)=\sum_{n=0}^M\sum_{m=-n}^n s_n^mY_n^m(\lambda,\mu)

のように展開して近似したい、というのがモチベーションです。ここに、\lambdaは経度、\mu=\sin\phiはサイン緯度(\phiが緯度)、Mは切断波数です。

球面調和関数は、Legendre陪関数P_n^m(\mu)を用いてY_n^m(\lambda,\mu)=P_n^m(\mu)e^{im\lambda}と書くことができます。Legendre陪関数の取り方にはいくつか流儀がありますが、ここでは直交関係が簡単に書けるようにするために、

P_n^m(\mu)=\sqrt{(2n+1)\frac{(n-|m|)!}{(n+|m|)!}}\frac{1}{2^n n!}(1-\mu)^{|m|/2}\frac{d^{n+|m|}}{d\mu^{n+|m|}}\left( (\mu^2-1)^n\right)

と取ることにします。このように定義されたLegendre陪多項式には\int_{-1}^1d\mu　P_n^mP_{n'}^m=2\delta_{n,n'}という直交関係があるので、球面調和関数には

\int_{-1}^1d\mu\int_0^{2\pi}d\lambda ~Y_n^m(Y_{n'}^{m'})^*=4\pi \delta_{n,n'}\delta_{m,m'}という直交関係があることになります。

　この直交関係を用いれば、正変換が定義できます。逆変換の定義の両辺に(Y_p^q)^*を掛けて球全体で積分することで

s_p^q=\frac{1}{4\pi}\int_{0}^{2\pi}d\lambda\int_{-1}^1d\mu~ g(\lambda,\mu)Y_p^q(\lambda,\mu)

\therefore~~s_n^m=\frac{1}{4\pi}\int_{0}^{2\pi}d\lambda\int_{-1}^1d\mu~ g(\lambda,\mu)P_n^m(\mu)e^{im\lambda}

を得ます。

　s_n^mの自由度について考えてみましょう。Y_n^mは n\geq0,~-n\leq m\leq nで定義されており、Y_n^{-m}=(Y_n^{m})^*の関係があるので、g(\lambda,\mu)が球上の実関数であれば、s_n^{-m}=(s_n^m)^*を満たします。よってs_n^mはM\geq m \geq 0の成分のみ求めれば良く、また任意のnに対してs_n^0が実数であることがわかります。

　さて、以上のことを計算機上で実行するためには適当に離散化する必要があります。離散フーリエ変換の際には適当に等間隔に格子点を取れば積分を正確に評価できたのですが、今回緯度方向にはLegendre陪多項式で展開されているため、別の取り方が良さそうです。そこで、以下の公式を使います。

  • Gauss-Legendreの積分公式
    • \muの2J-1次の多項式f(\mu)に対して、正確に\int_{-1}^1f(\mu)d\mu=\sum_{k=1}^Jw_kf(\mu_k)である。
    • ただし、\mu_k,~k=1,2,\dots,JはLegendre多項式P_J(\mu):=P_J^0(\mu)のJ個の零点で、-1\lt\mu_1\lt\mu_2\lt\dots\lt\mu_n\lt1
    • また、w_kはGauss重みで、w_k:=\frac{2\sqrt{4J^2-1}}{JP_{J-1}(\mu_k){P_J}^{'}(\mu_k)}

この公式を使うことによって、正変換の積分が正確に評価できます。すなわち、まず

G^m(\mu):=\frac{1}{2\pi}\int_0^{2\pi}g(\lambda,\mu)e^{-im\lambda}d\lambda

と置くと、この積分は経度方向にK個の等間隔の分点\lambda_k:=2\pi k/K,~~k=0,1,\dots,K-1を取って離散化すれば

G^m(\mu)=\frac{1}{K}\sum_{k=0}^{K-1}g(\lambda_k,\mu)e^{-im\lambda_k}

となります。これは(実)フーリエ正変換のルーチンを使うことで高速に計算できます。g(\lambda_k,\mu)を正変換すればm=0,1,\dots,K-1のK個の値が得られますが、m=0,1,\dots,Mまでしか使わないので、m=M+1,\dots,K-1の値は捨てましょう。(この時点では\mu方向には離散化されていませんが、これから見るように、\mu_j上でのみ計算すればいいことがわかります。)

　このようにして得られるG^m(\mu)を使えば、緯度方向の積分は

s_n^m=\frac{1}{2}\int_{-1}^1 G^m(\mu)P_n^m(\mu)d\mu

となりますが、Gauss-Legendreの積分公式より

s_n^m=\frac{1}{2}\sum_{j=1}^J w_jG^m(\mu_j)P_n^m(\mu_j)

と計算できます。以上のことをまとめれば、正変換は

g(\lambda_k,\mu_j) \xrightarrow{FFT} G^m(\mu_j) \rightarrow s_n^m

のように計算を回すことになります。

 

　逆変換はどうでしょうか。逆変換では、

g(\lambda_k,\mu_j)=\sum_{n=0}^M\sum_{m=-n}^n s_n^m P_n^m(\mu_j)e^{im\lambda_k}

を計算することになります。これもまずLegendre逆変換をしてからフーリエ逆変換を使うことを見越して、まず総和の順序を

g(\lambda_k,\mu_j)=\sum_{m=-M}^M\sum_{n=|m|}^M s_n^m P_n^m(\mu_j)e^{im\lambda_k}

のように入れ替えます。ただし、ここでは

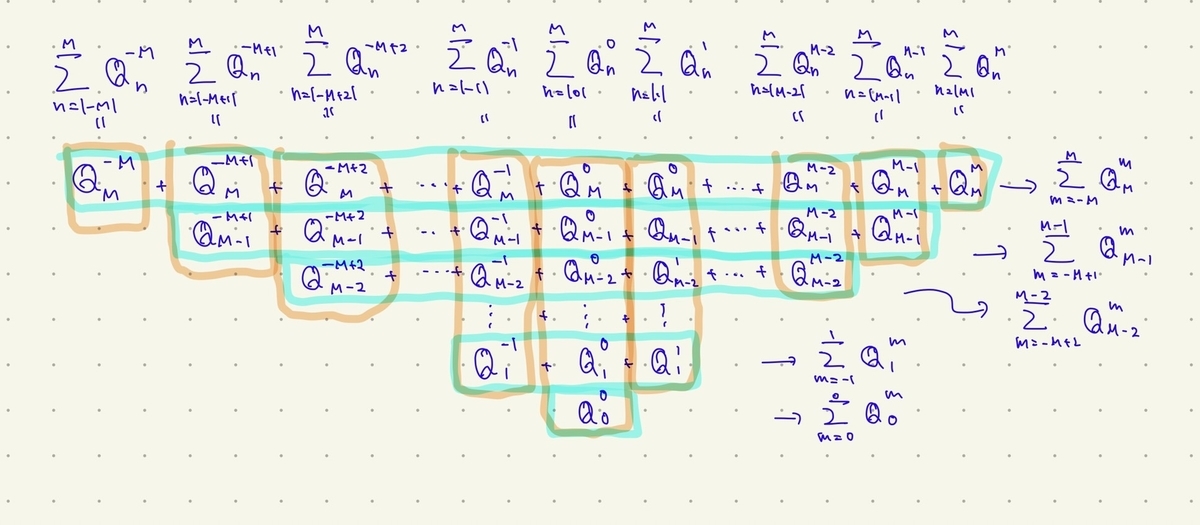
\sum_{n=0}^M\sum_{m=-n}^n Q_n^m=\sum_{m=-M}^M\sum_{n=|m|}^M Q_n^m

となることを使いました。あまり自明な感じがしませんが、これは図1のように全部書き下すと直感的に理解できます。先に横方向の和を取れば左辺に、先に方向の和を取れば右辺になります。

図1.和の順序の入れ替え

そして、m\geq0なるmに対してG^m(\mu)を

G^m(\mu_j)=\sum_{n=|m|}^Ms_n^mP_n^m(\mu_j)

と定義すれば、逆変換の式は

g(\lambda_k,\mu_j)=\sum_{m=-M}^MG^m(\mu_j)e^{im\lambda_k}

となりますが、これは切断波数M、分点数Kの(実)フーリエ逆変換となっていて、高速に計算できます。普通のFFTルーチンで計算できる形に変形してみましょう。まずg(\lambda_k,\mu_j)は実数であることから、G^{-m}(\mu_j)=(G^m(\mu_j))^*がわかります。

さらにe^{-im\lambda_k}=e^{im\lambda_{K-k}}であることから、負の波数を持つ成分を

g(\lambda_k,\mu_j)=\sum_{m=0}^MG^m(\mu_j)e^{im\lambda_k}+\sum_{m=1}^MG^{-m}(\mu_j)e^{-im\lambda_k}

=\sum_{m=0}^MG^m(\mu_j)e^{im\lambda_k}+\sum_{m=1}^M(G^{m}(\mu_j))^*e^{im\lambda_{K-k}}

=\sum_{m=0}^MG^m(\mu_j)e^{im\lambda_k}+\sum_{m=K-M}^{K-1}(G^{K-m}(\mu_j))^*e^{im\lambda_{k}}

のように正波数の領域に押し込めることができます。したがって、

H^m(\mu_j)=G^m(\mu_j) ~(m=0,1,\dots,M)

H^m(\mu_j)=(G^{K-m}(\mu_j))~(m=K-M,K-M+1,\dots,K-1)

H^m(\mu_j)= 0~(otherwise)

のようにH^mを定義すれば、

g(\lambda_k,\mu_j)=\sum_{m=0}^{K-1}H^m(\mu_j)e^{im\lambda_k}

と、普通の(実)フーリエ逆変換のルーチンで計算することができます。以上のことをまとめると、

s_n^m\rightarrow G^m(\mu_j)(\rightarrow H^m(\mu_j))\xrightarrow{FFT^{-1}} g(\lambda_k,\mu_j)

と計算を回すことになります。

実装するぜ

　実装しましょう。しかし変換を行う前に

  1. Legendre多項式P_J(\mu)のJ個の零点\mu_j
  2. Legendre陪多項式の値P_n^m(\mu_j),~(0\leq n\leq M,0\leq m\leq n)

を予め求めておいたほうが効率が良さそうです*4。ですがLegendre陪多項式の定義式を思い出すと、n+|m|階微分が含まれていて面倒です。また、零点を求めるときにNewton法を使うことにすれば、Legendre多項式の1階微分も必要になります。そこで必要になるのが以下の漸化式です。

  • P_n^m=\sqrt{\frac{4n^2-1}{n^2-m^2}}\mu P_{n-1}^m-\sqrt{\frac{2n+1}{2n-3}}\sqrt{\frac{(n-1)^2-m^2}{n^2-m^2}}P_{n-2}^m~~\dots\dots(A)
  • (1-\mu^2)\frac{d}{d\mu}P_n=n\sqrt{\frac{2n+1}{2n-1}}P_{n-1}-n\mu　P_n~~\dots\dots(B)

また、Legendre陪多項式の定義から、直ちに次のことがわかります。

  • P_m^m=\frac{\sqrt{(2m+1)!}}{m!}\left(\frac{1-\mu^2}{4}\right)^{m/2}~~\dots\dots(C)
  • P_{m+1}^m=\mu\sqrt{2m+3}P_m^m(\mu)~~\dots\dots(D)

 

　まず、零点の求め方を考えます。Newton法を使って零点を求めるとすれば、ある適当な初期推定値\mu_j^0=\cos\left(\frac{\pi(j-1/4)}{J+1/2}\right)*5からP_J(\mu_j^0),~~P_J'(\mu_j^0)=\frac{d}{d\mu}P_J(\mu_j^0)を求め、更に漸化式

\mu_j^{l+1}=\mu_j^l-\frac{P_J(\mu_j^{l})}{P_J'(\mu_j^{l})}

を適当な回数回して、P_J(\mu_j^l)ないしは|\mu_j^{l+1}-\mu_j^{l}|が十分小さくなったら反復を終える、という作業をします。ここではある与えられた\muに対してP_J(\mu)を求める必要がありますが、それは漸化式(A)においてm=0とした式から再帰的に求められます。ただし、P_0(\mu)=1,~~P_1(\mu)=\sqrt{3}\muを利用します。

再帰的にと言っているので(fortranなら)recursive属性のついた再帰関数を実装したくなるところですが、お察しの通りそれをやると計算量がえげつないことになるので、動的計画法チックに書いたほうが高速に計算できます。

P_J(\mu)が求まってしまえば漸化式(B)からP_J'(\mu)も求められるので、以上によって零点を求めることができました。適当な配列に突っ込んでおきましょう。

 

　各\mu_j上のLegendre陪多項式の値P_n^m(\mu_j)の方はどうでしょうか。ここでは、まず対角成分P_m^m(\mu_j)とそのひとつ上の成分P_{m+1}^mをそれぞれ式(C),(D)によって求めて、それらの値から漸化式(A)を用いて上に登っていくという方針で求めます*6。図示すれば、図2.のようになります。

図2. Legendre陪多項式の構築順序

 

Legendre陪多項式をどのように配列に格納するか、という問題が残っています。n,~mについては0\leq m \leq M,~~m\leq n\leq Mという範囲で定義されているので、全部でJ\sum_{k=0}^M k+1=J(M+1)(M+2)/2個をしまうことになります。正変換と逆変換の式をグッと睨むと、j\gt n \gt mの順番に内側のループでたくさん呼び出されているので、それを考慮して格納したほうが良さそうです。ここでは\verb#Ass_leg#(1:J,0:(M+2)(M+1)/2-1)と定義して、図3のようにしまいました。

図3.Legendre陪多項式の格納順序


P_n^m(\mu_j)は\verb#Ass_leg#(j,idx_m^n)に格納されることになります。ただしidx_n^m:=\sum_{k=M-m+2}^{M+1}k+n-m+1-1

=m(2M-m+3)/2+n-mです。

　

　以上でLegendre陪多項式の構築ができたので、変換が実装できたことになります。やった～～

可視化、ベンチマーク結果

　さて、以上の変換を実装し、スペクトルデータからグリッドデータ(S2G, Spectrum to Gridなので)に変換した結果が図4.です。

図4. S2G結果

ここでは、ある(n,m)にのみs_n^mを1にして、それ以外のスペクトル値を全部ゼロにして変換しました。こうすれば、球面調和関数の(実部の)値を得ることができます。量子力学の教科書などでよく見るような結果が得られているので、まあいい感じなんじゃないんでしょうか。

ちなみに可視化にはParaviewを使いました。ググれば使い方が出てくる程度の使い方しかしていません。でもそのうちParaviewを使って二次元球面上の実験結果の可視化みたいなことをやろうも思っていて、もしそれができたらParaviewのことも記事にしたいとは思ってます*7。

 

　さて、計算時間の方はどうでしょうか。教授から借りてるノートパソコンでベンチマークしました。スペックはCPU:i7-2640M, メモリ:8GBです。世界最速のSHTライブラリであるところのispack*8との比較結果を以下に示します。表中の値は計算時間[sec]です。

切断波数 M=511 M=1023 M=2047
telibrary*9 bwd 0.599 4.69 -
ispack bwd 0.019 0.0579 0.392
telibrary fwd 0.731 5.65 -
ispack fwd 0.0093 0.0469 0.356

惨敗で草

ispackより2桁、ひどいときで3桁くらい遅いです。私のライブラリではM=2047のときはもはや計算が不可能でした。P_n^m(\mu_j)を素直に求めて素直にメモリに突っ込むように実装したので、切断波数がデカいとメモリに乗らなくなるのが原因です。M=2047だと、Legendre陪多項式だけでだいたい8*2048*2049*2050/2[bytes]≒34.4[GB]の記憶容量が必要になります。正気か？

図5. デカすぎる配列は数値計算スキームを滅ぼす

 

高速化に向けて

　前節で見たように、素人が見様見真似で実装しただけではカスみたいな遅さのプログラムが出来上がることがわかりました。FFTの場合は適当に実装してもまあまあな速度が出るのでフルスクラッチの数値計算スキームを作ることができたのですが、SHTはなかなか一筋縄ではいかなそうです。

　このままだと悔しいので当然高速化していきたい訳ですが、どういう方向があるのか？という話を最後にちょっとだけしたいと思います。

　今回の実装では並列処理を全く挟んでいない、単純極まりないコードを書きました。普段使うような計算機では、OpenMPなどを使えばあまり複雑なことを考えずに並列計算をすることができるので、そうすれば定数倍程度は速くなりそうです。

　また、前節で見たように、Legendre陪多項式を予め求めてしまうとクソデカ配列になってしまい、キャッシュどころかメモリにも載らなくなってしまう、という問題点があります。これに関しては、変換するごとにLegendre陪多項式の値を求めることで解決できるらしいです。詳しくは注釈で紹介した論文をご覧ください。また、「球面調和関数変換　キャッシュ」などで検索すると、ispack製作者であるところの石岡圭一氏のスライドが色々出てきます。この論文ではテクニカルな漸化式と命令を用いてLegendre陪多項式の計算量を通常の1/3程度に抑えていますが、そこまでしなくてもうまいことやったらまあまあ速くなるような気がします。

　また、ナイーブな手法としては、ガウス緯度の偶奇性を利用してjについての和を半分にするという手法もあるようです。いずれにせよ、できることはまだまだありそうです。

まとめ

  • クソ遅いSHTライブラリを構築した
  • 悔しい
  • SHT(Sugoku Hayai Transform)にしたい
  • そうでなくてもせめて卒業研究で使える程度の速さにはしたいので、修行を積みます

　

*1:例えばこういうのを実装していました。対流不安定な成層上でベナール対流が発達する様子です。上が温度場、下が流線関数を描いています。

アニメーション1. 味噌汁の様子　かわいいね


鉛直方向は境界条件の問題からフーリエ級数じゃなくサイン級数で展開する必要があり、そのためにFSTとFCTを実装しました。

*2:Spherical Harmonic Transformの略。HTTみたいですね。

*3:てかこの令和の時代に自分でSHTのライブラリを作りたいなんて人がそもそもいないんでしょうね。どのライブラリもゴリゴリにチューンされてて勝ち目なんてないし。

*4:ただ、高速化の観点から見ると、Legendre陪多項式の値は全部求めるとクソでかい配列になって、キャッシュに乗らなくなってしまうので、変換のたびに求めたほうが効率がいいらしいです。詳しくはIshioka, K. (2018). A new recurrence formula for efficient computation of spherical harmonic transform. In Journal of the Meteorological Society of Japan (Vol. 96, Issue 2, pp. 241–249). Meteorological Society of Japan. https://doi.org/10.2151/jmsj.2018-019 を読んでください。

*5:なんかこういう初期値を取るといい感じに求めることができるっぽいです

*6:P_n^mの上付き添字を動かす漸化式をどっかから引っ張ってきて、P_nの値からP_n^mを求めようとしたこともあったのですが、それをすると計算誤差がデカくなるので、上の手法を採用しました。

*7:その前にSHTライブラリを高速化しないと何もできない

*8:

www.gfd-dennou.org

*9:てれじょんのライブラリ、略しててらいぶらり

Gnuplotで等値線付きアニメーションを描画する

これはなに

　おはこんばんにちはてれじょんです。もう8月60日ですね。もう数日で8月が終わって10月になるのが信じられません。みなさんはこの夏休み何をしましたか？私は実家で皿洗いと風呂掃除をやらされてやらせて頂いて、免許をとって睡眠して食事していたら終わっていました。なんで？休み前半の進捗は結構いい感じでしたが、後半の進捗を自動車学校に破壊されたのが非常に遺憾です。まあ進捗が微妙になったのは自動車学校のせいではなく自分のせいですが……

　さて本題ですが、今日はGnuplotを使ってこういうgifアニメを作っていきます。gnuplotのことは記事にするつもりはあんまりなかったのですが、結構複雑になってきて忘れそうなので記事にしておきます。

f:id:jhonson1415:20200929143054g:plain

図1.こういうのを作ります

　ちなみに上のグラフは地学部気象班のtwitterアカウントでも投稿した浅水方程式の数値解です。境界は自由端としてt=0で中央に正弦波を与えています。

 

作るぜ

作っていきます。作りたいのは山々ですが、まずインプットするデータの体裁を整えていきます。

x-y平面上の格子点におけるzの値が与えられ、それらが時間変化するような場合を考えましょう。格子点の座標は(x_i,y_j)(0<=i<=l,0<=j<=m)とします。このとき、インプットするデータは

####x,y,z####

x_0 y_0 z(x_0,y_,t_0)

x_1 y_0 z(x_1,y_0,t_0)

...

x_l y_0 z(x_l,y_0,t_0)

x_0 y_1 z(x_0,y_1,t_0)

x_1 y_1 z(x_1,y_1,t_0)

...

x_l y_m z(x_l,y_m,t_0)

 

 

x_0 y_0 z(x_0,y_,t_1)

x_1 y_0 z(x_1,y_0,t_1)

...

x_l y_0 z(x_l,y_0,t_1)

x_0 y_1 z(x_0,y_1,t_1)

x_1 y_1 z(x_1,y_1,t_1)

...

x_l y_m z(x_l,y_m,t_1)

 

 

x_0 y_0 z(x_0,y_,t_n)

x_1 y_0 z(x_1,y_0,t_n)

...

x_l y_0 z(x_l,y_0,t_n)

x_0 y_1 z(x_0,y_1,t_n)

x_1 y_1 z(x_1,y_1,t_n)

...

x_l y_m z(x_l,y_m,t_n)

#########

のように、時間ステップが次のものに移るたびに2行空行を入れておきます。これだけでOKです。

 

　gnuplotに移り、

gnuplot>set term gif animate

gnuplot>set output "nami.gif"

で出力をgifアニメにして、適当な名前をつけます。必要に応じて

gnuplot>set xrange[0:1]

gnuplot>set yrange[0:1]

などで範囲を指定します。

 

で、次に等値線の設定をします。インプットするデータは離散的なデータなので、平面のデータを作らなければなりません。それを代行してくれるのがdgrid3dです。

gnuplot>set dgrid3d 50,50,4

をするとグリッドデータを作ってくれます。便利ですね。

最初2つの引数はそれぞれx,y方向の格子数、3つめの引数は格子点の距離からの重みをいくらにするかを指定する引数です。このとき、格子点からの距離の4乗の逆数で重みがかかります。

また等値線間隔を

gnuplot>set cntrparam levels incremental -0.1,0.02,0.1

で指定します。このとき等値線の最小値は-0.1,間隔は0.02,最大値が0.1になります。この他にも

・set cntrparam levels autoでは等値線の本数が自動で設定されます

・set cntrparam levels ～では等値線の本数が～本になります

最後に

gnuplot>set contour

で等値線を出力するようセットします。これで等値線の設定がオワリました。

 

今度はアニメーションの設定です。次のような中身のテキストファイルを(適当な名前).pltで保存します。

##

if(exist("n")==0 || n<0)n=n0
splot "output3.d" index n using 1:2:3 w l
n=n+dn
if(n<n1)reread
undefine n

##

簡単なループなのでノリで理解できると思います。

これを実行すると、splot "output3.d" index n using 1:2:3 w l

のところでインプットデータの上からnつ目のブロックが読み込まれ、t_nでのグラフが出力されます。

n0が初期値でn1が読み込むブロックの総数なので

gnuplot>n0=1

gnuplot>n1=200

gnuplot>dn=1

 とか適当に設定しておきます。

 

最後に、 

gnuplot>load "(名前).plt"

を実行します。すると現在のディレクトリにファイルが出力されるという算段です。

 

まとめ

####

if(exist("n")==0 || n<0)n=n0
splot "output3.d" index n using 1:2:3 w l
n=n+dn
if(n<n1)reread
undefine n

###

をplt形式で現在のディレクトリに保存、んで以下の図のように実行していくと出力されます。便利だね。

f:id:jhonson1415:20200929181304p:plain

図2.コマンドの様子

 

f:id:jhonson1415:20200929183130g:plain

図3.たのしいね

参考サイト

以下のサイトを参考にさせていただきました。ありがとうございました。

kengo700.hatenablog.com

 

www.propulsion.kuaero.kyoto-u.ac.jp

kuroneko-momotaro.blogspot.com

Gauss-Seidel法と二次元Laplace方程式の数値解法について

これはなに

　おはこんばんにちはてれじょんです。9月に入ると陸の孤島ではクソデカ積乱雲くんや激高気温くんが多く観測され、ようやく夏という風情が出てきました(まじでなに？)。8月もまあまあ暑かったですが、陸の孤島は9月もクソ暑くなりそうなので泣いています。太平洋高気圧、嘘だよな……？
　さて今回はGauss-Seidel法による連立方程式の反復解法について書いて、さらにそれを用いてLaplace方程式を数値的に解いていきたいと思います。私が参考にした本ではLaplace方程式の数値解を求めるときにSOR法を用いていましたが、収束条件の証明をよく理解していない(したがって最適なパラメーターのとり方がよく分かってない)のでGauss-Seidel法を使うことにします。

Gauss-Seidel法 is 何

　前回は、名前がよく似たGauss-Jordan法を使って連立方程式を解きました。詳しい説明は前回の記事に譲りますが、これは手計算と同じように行基本変形を繰り返していって解を求める方法でした。一方ここでは行列の変形は行わず、未知変数と同じ数の漸化式をつくり、適当な初期値から始めて逐次値を代入し、誤差項がある値\epsilon >0より小さくなったら計算を打ち切るという方法で近似解を求めていきます。あくまで求めているのは近似解なので、これを反復法と言ったりもするらしいです。前回扱ったのは直接法です。

　具体的な操作を見ていきましょう。まず一般的に、n次実正方行列A \in Mat_n(\mathbb{R})とn行縦ベクトル\boldsymbol{b} \in \mathbb{R}^nを用いてA\boldsymbol{x}=\boldsymbol{b}と書けるn元一次連立方程式の解き方を考えます。適当な初期値\boldsymbol{x}^{(0)}=(x_1^{(0)},x_2^{(0)},\cdots,x_n^{(0)})を作り、漸化式


{\displaystyle \begin{eqnarray} \left\{ \begin{array}{l} a_{11}x_1^{(\nu +1)}+a_{12}x_2^{(\nu)}+\cdots+a_{1n}x_n^{(\nu)}&=b_1 \\ a_{21}x_1^{(\nu +1)}+a_{22}x_2^{(\nu+1)}+\cdots+a_{2n}x_n^{(\nu)}&=b_2 \\ \vdots \\ a_{n1}x_1^{(\nu +1)}+a_{n2}x_2^{(\nu+1)}+\cdots+a_{nn}x_n^{(\nu+1)}&=b_n \end{array} \right. \end{eqnarray} }


に上からに代入していくことで順次\boldsymbol{x}^{(1)},\boldsymbol{x}^{(2)},\cdotsを得ます。何度か反復を行うと\underset{1\leq i \leq n}{\max} |b_i-\sum_{j=1}^n a_{ij}x_{j}^{(\nu)}|<\epsilonとなるので、十分\epsilonが小さくなったときに収束したとみなして解を得ます。これがGauss-Seidel法です。

は？？？？？？？？？

おそらく皆さん「これでなんで収束するって言えるの？」と思ったでしょう。私も思いました。色々調べてみたりもしましたが、大抵の場所では収束性についてさして言及していなかったのでちょっと丁寧に書いてみたいと思います。
　当然この方法は一般の連立方程式に対して収束するものではないので、解を得るためにはいくつかの条件が必要です。そこで出てくるのが以下の2つの定理です。

Th.1
H \in Mat_n(\mathbb{R}),~~\boldsymbol{x}^{(\nu)},\boldsymbol{c} \in \mathbb{R}^nとする。このとき、スペクトル半径\rho(H)(:=\max{|\lambda|},~\lambdaはHの固有値)に対して\rho(H)<1ならば反復法\boldsymbol{x}^{(\nu+1)}=H\boldsymbol{x}^{(\nu)}+\boldsymbol{c}は\boldsymbol{x}=H\boldsymbol{x}+\boldsymbol{c}の一意解に収束する。

【証明】
\rho(H)<1ならばE-Hは逆行列をもち、(E-H)^{-1}=E+H+H^2+\cdotsである。
したがって\boldsymbol{x}=(E-H)^{-1}\boldsymbol{c}より、\boldsymbol{x}=H\boldsymbol{x}+\boldsymbol{c}は一意解を持つ。それを\boldsymbol{\alpha}とする。このとき上記の反復法は
\boldsymbol{x}^{(\nu)}-\boldsymbol{\alpha}=H(\boldsymbol{x}^{(\nu-1)}-\boldsymbol{\alpha})=H^\nu(\boldsymbol{x}^{(0)}-\boldsymbol{\alpha})\underset{\nu\rightarrow\infty}{\rightarrow}\boldsymbol{0}
となるので、題意は示された。


Th.2
A \in Mat_n(\mathbb{R})が狭義優対角行列または既約優対角行列ならば、Gauss-Seidel法は任意の初期値に対してA\boldsymbol{x}=\boldsymbol{b}の解に収束する。

【証明】
D,L,U\in Mat_n(\mathbb{R})を
D=\begin{bmatrix} a_{11} &0 & \cdots & 0\\ 0 & a_{22}&\cdots &0 \\ \vdots&\vdots&\ddots &\vdots \\ 0&0&\cdots&a_{nn} \end{bmatrix}~~,L=\begin{bmatrix} 0 &0 & 0&\cdots & 0\\ a_{21} & 0&0&\cdots &0 \\ a_{31}&a_{32}&0&\cdots&0 \\ \vdots&\vdots&\vdots&\ddots &\vdots \\ a_{n1}&a_{n2}&a_{n3}&\cdots&0 \end{bmatrix},\\U=\begin{bmatrix} 0 &a_{12} & a_{13}&\cdots & a_{1n}\\ 0 & 0&a_{23}&\cdots &a_{2n} \\ 0&0&0&\cdots&a_{3n} \\ \vdots&\vdots&\vdots&\ddots &\vdots \\ 0&0&0&\cdots&0 \end{bmatrix}

で定義する。このとき、Gauss-Seidel法の漸化式より

\begin{bmatrix} a_{11} &0 & 0&\cdots & 0\\ a_{21} & a_{22}&0&\cdots &0 \\ a_{31}&a_{32}&a_{33}&\cdots&0 \\ \vdots&\vdots&\vdots&\ddots &\vdots \\ a_{n1}&a_{n2}&a_{n3}&\cdots&a_{nn} \end{bmatrix}\begin{bmatrix} x_1^{(\nu+1)} \\ x_2^{(\nu+1)} \\ x_3^{(\nu+1)} \\ \vdots \\ x_n^{(\nu+1)}\end{bmatrix}+\begin{bmatrix} 0 &a_{12} & a_{13}&\cdots & a_{1n}\\ 0 & 0&a_{23}&\cdots &a_{2n} \\ 0&0&0&\cdots&a_{3n} \\ \vdots&\vdots&\vdots&\ddots &\vdots \\ 0&0&0&\cdots&0 \end{bmatrix}\begin{bmatrix} x_1^{(\nu)} \\ x_2^{(\nu)} \\ x_3^{(\nu)} \\ \vdots \\ x_n^{(\nu+1)}\end{bmatrix}=\boldsymbol{b}
\therefore (D+L)\boldsymbol{x}^{(\nu+1)}+U\boldsymbol{x}^{(\nu)}=\boldsymbol{b} \\ \boldsymbol{x}^{(\nu+1)}=-(D+L)^{-1}U\boldsymbol{x}^{(\nu)}+(D+L)^{-1}\boldsymbol{b}

を得る。故に、Th.1より\rho(-(D+L)^{-1}U)<1を示せばよく、そのために固有値問題

-(D+L)^{-1}U\boldsymbol{x}=\lambda \boldsymbol{x} ~~\Leftrightarrow~~-U\boldsymbol{x}=\lambda (D+L)\boldsymbol{x}

を考え、\max{|\lambda|}<1を示すことにする。

(i)狭義優対角のとき
|x_m|=\underset{1\leq j \leq n}{\max}|x_j|となるようなmを取る。
このとき、-U\boldsymbol{x}=\lambda (D+L)\boldsymbol{x}の第m成分を考えて

-\sum_{j\geq m+1} a_{mj}x_j=\lambda a_{mm}x_m+\lambda \sum_{j\leq m-1}a_{mj}x_j
\therefore ~~ -\lambda a_{mm}x_k=\underset{j\geq m+1}{\sum}a_{mj}x_j+\lambda \sum_{j\leq m-1}a_{mj}x_j

ここで、^\exists|\lambda|\geq 1を仮定すると、三角不等式より

\begin{array}{l} 　|\lambda||a_{mm}||x_m| & \leq |\lambda||\sum_{j\neq m}a_{mj}x_j| \\ &\leq |\lambda|\sum_{j \neq m}|a_{mj}||x_j| \\ &\leq |\lambda||x_m|\sum_{j \neq m} |a_{mj}| \end{array}

\therefore ~~ |a_{mm}|\leq \sum_{j\neq m}|a_{mj}|

となって、Aが狭義優対角行列であることに反する。

(ii)既約優対角のとき
狭義優対角のときと同様にx_mをとり、J=\left\{j~|~|x_j|=|x_m|\right\}とする。
|\lambda|\geq 1として矛盾を導く。

・J=\left\{1,2,\cdots,n\right\}のとき
このとき、(i)と全く同様にして
^\forall k,~ |a_{kk}|\leq \sum_{j\neq k}|a_{kj}|
が言えるので既約優対角性に反する。

・そうでないとき
^\exists x_j ~s.t.~|x_m|>|x_j|

このとき

|\lambda||a_{mm}||x_m|\leq |\lambda|\sum_{j\neq m}|a_{mj}||x_j|\leq|\lambda|(\sum_{j\in J}|a_{mj}||x_j|+\sum_{j\notin J}|a_{mj}||x_j|)~~\cdots(1)

が成立する。ところで、j \notin Jならばa_{mj}=0である。実際、もしa_{mj}\neq 0となるようなj \in Jが存在するとすれば

\sum_{j\notin J}|a_{mj}||x_j|<\sum_{j\notin J}|a_{mj}||x_m|

なので、(1)より

|\lambda||a_{mm}||x_m|<|\lambda||x_m|\sum_{j\neq m}|a_{mj}| \\ \therefore ~~ |a_{mm}|<\sum_{j\neq m}|a_{mj}

となって、既約優対角性に反する。したがって、

m\in J ,~ j\notin J \Rightarrow a_{mj}=0

が分かり、Aが既約であることに反する。以上より|\lambda|<1であり、題意は示された。


証明長すぎん？？？tex打ちがめんどい

まあ無事Th.2が示されたので良しとしましょう。これより、狭義優対角または既約優対角行列に対してはGauss-Seidel法が使えることが分かりました。でもまだなんか胡散臭いような気がする。

二次元Laplace方程式を解く(理論の説明)

　さて、ようやく本題です。ここではDirichlet境界条件下におけるLaplace方程式\frac{\partial^2\phi}{\partial x^2}+\frac{\partial^2\phi}{\partial y^2}=0を数値的に解いていこうと思います。簡単のため、0\leq x,y,\leq 1の正方形領域で考えることとし、境界条件は

{\displaystyle \begin{eqnarray} \phi(x,y)=\left\{ \begin{array}{l} 　0&(x=0,1~or~y=1)\\ \sin(2\pi x)&(y=0) \end{array} \right. \end{eqnarray}}

とします。当然計算機に解かせるには離散化しなきゃいけません。正方形領域をx方向にn等分、y方向にm等分して、その分点をそれぞれ\left\{x_0=0,x_1=1/n,x_2,x_3,\cdots,x_n=1\right\}、\left\{y_0=0,y_1=1/m,y_2,y_3,\cdots,y_m=1\right\}とおきます。便宜上、\phi(x_i,y_j)=\phi_{i,j}と書いて、分点の間隔を\Delta x=1/n,~\Delta y=1/mと置きます。このとき、\phiをTaylor展開することで

\begin{array}{l} \phi_{i+1,j}&=\phi(x_i+\Delta x,y_j) \\ &=\phi_{i,j}+\frac{\partial\phi}{\partial x}\Delta x+\frac{1}{2}\frac{\partial^2\phi}{\partial x^2}\Delta x^2+\frac{1}{6}\frac{\partial^3\phi}{\partial x^3}\Delta x^3+O(\Delta x^4) \\ \phi_{i-1,j}&=\phi(x_i-\Delta x,y_j) \\ &=\phi_{i,j}-\frac{\partial\phi}{\partial x}\Delta x+\frac{1}{2}\frac{\partial^2\phi}{\partial x^2}\Delta x^2-\frac{1}{6}\frac{\partial^3\phi}{\partial x^3}\Delta x^3+O(\Delta x^4) \\ \end{array}

を得ます。片々足してよしなにしてやれば

\left.\frac{\partial^2\phi}{\partial x^2}+\frac{\partial^2\phi}{\partial y^2}\right\|_{x=x_i,y=y_j}=\frac{\phi_{i+1,j}-2\phi_{i,j}+\phi_{i-1,j}}{\Delta x^2}+\frac{\phi_{i,j+1}-2\phi_{i,j}+\phi_{i,j-1}}{\Delta y^2}+O(\Delta x^2)+O(\Delta y^2)

を得ます。二次以上の項は無視して良さそうなので無視して、

\frac{\phi_{i+1,j}-2\phi_{i,j}+\phi_{i-1,j}}{\Delta x^2}+\frac{\phi_{i,j+1}-2\phi_{i,j}+\phi_{i,j-1}}{\Delta y^2}=0 \\ \therefore~~\frac{\Delta y^2}{2(\Delta x^2+\Delta y^2)}(\phi_{i+1,j}+\phi_{i-1,j})+\frac{\Delta x^2}{2(\Delta x^2+\Delta y^2)}(\phi_{i,j+1}+\phi_{i,j-1})-\phi_{i,j}=0

ここで

\frac{\Delta y^2}{2(\Delta x^2+\Delta y^2)}=\frac{n^2}{2(n^2+m^2)}:=p,~\frac{\Delta x^2}{2(\Delta x^2+\Delta y^2)}=\frac{m^2}{2(n^2+m^2)}:=q

とおけば、上の式は

p(\phi_{i+1,j}+\phi_{i-1,j})+q(\phi_{i,j+1}+\phi_{i,j-1})-\phi_{i,j}=0

となります。だいぶ見通しが良くなりましたね。これと境界条件をあわせれば、全体で(n-1)(m-1)+2(n+1)+2(m-1)=(n+1)(m+1)本の連立方程式を成します。未知変数は(n+1)(m+1)個なのであとはこの連立方程式を解けば良いことが分かります。

解くぜ！

　実装しましょう。解くために\phi_{i,j}を一本のベクトルに格納してみます。うまいこと格納してやれば実装も楽になると思うのですが、いい方法が思い浮かばなかったので雑に格納してみます。上で得た(n+1)(m+1)本の連立方程式をA\boldsymbol{x}=\boldsymbol{b}と書いて

\boldsymbol{x}=(\phi_{0,0},\phi_{1,0},\cdots,\phi_{n,0},\phi_{0,1},\phi_{1,1},\cdots,\phi_{n,1},\cdots\cdots,\phi_{0,m},\phi_{1,m},\cdots,\phi_{n,m})^T

と突っ込んでみます。\phi_{i,j}は\boldsymbol{x}の第i+1+(n+1)j成分になっています。ただし、境界条件上の\phiの値は分かっているのでそこにははじめから値を入れておいて、残りのところには初期値として0を入れます。i+1+(n+1)j:=lと置いてみると、A\boldsymbol{x}=\boldsymbol{b}の第l成分(ただし\boldsymbol{x}の第l成分は未知とします)は

x_l-p(x_{l+1}+x_{l-1})-q(x_{l+n+1}-x_{l-n-1})=0

となります。こいつをGauss-Seidel法の漸化式とみなせば実装できますね。AがTh.2の条件を満たすことの証明は省略します。(多分)サクッとできるので。
んで、実装したコードは以下のようになりました。

module globals
   real(8),parameter :: pi=3.141592653589793d0
end module globals

module subprog
   use globals
   implicit none
contains
   function l(i,j,n) result(k)
      integer,intent(IN) :: i,j,n
      integer k
      k=i+1+(n+1)*j
   end function l
end module subprog

program main
   use globals
   use subprog
   implicit none
   integer :: n,m,i,j,ln,fo=11
   real(8),allocatable :: x(:)
   real(8) p,q,dx,dy,ep,tmp,t1,t2

   ep=0.000001d0
   write(*,*)"input step n(x-axis),m(y-axis)"
   read(*,*)n,m
   allocate(x((n+1)*(m+1)))
   x(1:(n+1)*(m+1))=0.0d0
   p=dble(n)**2/2.0d0/(dble(n)**2+dble(m)**2)
   q=dble(m)**2/2.0d0/(dble(n)**2+dble(m)**2)
   dx=1.0d0/dble(n)
   dy=1.0d0/dble(m)
   
   do i=0,n
      x(l(i,0,n))=sin(2.0d0*pi*dx*dble(i))
   enddo
   
   call cpu_time(t1)

1  do i=1,n-1
      do j=1,m-1
         ln=l(i,j,n)
         x(ln)=p*(x(ln+1)+x(ln-1))+q*(x(ln+n+1)+x(ln-n-1))
      enddo
   enddo

   do i=1,n-1
      do j=1,m-1
         ln=l(i,j,n)
         tmp=abs(x(ln)-p*(x(ln+1)+x(ln-1))-q*(x(ln+n+1)+x(ln-n-1)))
         if(tmp>=ep)then
            goto 1
         else
            if(i/=n-1 .or. j/=m-1)then
               CYCLE
            endif
         endif
      enddo
   enddo

   call cpu_time(t2)

   write(*,*)"cal_time=",t2-t1

   open(fo,file="output.d")
   do i=0,n
      do j=0,m
         ln=l(i,j,n)
         write(fo,*)dx*dble(i),dy*dble(j),x(ln)
      enddo
      write(fo,*)" "
   enddo
   close(fo)

end program main

解析結果

n=m=100としたときの解析結果は以下のようになりました。

f:id:jhonson1415:20200909102413p:plain
図1.解析結果

これの計算時間はだいたい0.21秒くらいだったので、概ねO((nm)^2)よりやや少ないくらいで計算できてると思います。(私のノートPCではO(10^8)の計算時間が0.25秒くらいでした)。

最後に

\LaTeX打ちがめんどい大変でした。記事の後半雑になってアレですがまあ良いでしょう。誤植とかおかしいところとかあったら言ってください。多分あります。自動車学校に収容されたので進捗のペースが落ちていますが、のんびりやっていきたいです。

参考文献

・数値計算のためのFortran90/95プログラミング入門(第2版)、牛島 省、森北出版、2020
・数値解析入門[増訂版]、山本哲朗、サイエンス社、2003

最小二乗法を実装した話


これはなに？

　おはこんばんにちはてれじょんです。厳しい暑さが続いていますが皆さんお元気でしょうか？私は陸の孤島秋田に帰省しているのでそこまできつい暑さでは無いのですが、それでもまあ暑いです。死なない程度に生きていきたいものです。天気図も書きたいものです。(うちのスーパーコンピューターであるところの"1-LOUGH"*1 が秋田に無いので自明に録音ができなくて詰んでいます。助けて。)
　ところで皆さんはまちカドまぞくを知っていますか？悪いことは言わないので知らないヒトは今すぐ見てください。今日ツイッターを見ていたところ「2期決定！」というのを発見して特大の喜びをしたのですが、リークだと知り一瞬で真顔に戻りました。公式で発表されてないことを確認する前に拡散した自分も悪いんですが、好きな作品の喜ばしい発表に対して素直に喜べないのは本当に本当に本当に本当に悲しい限りなので、リーカーは潔く自決してほしいですね。私も自決するべきですが。
　さて本題ですが、今日はFortranの教科書*2にさらっと書かれていた最小二乗法を実装しました。点列を入力して偏微分して得られる連立方程式を解く……という簡単なステップですが、連立方程式を解くときにGauss-Jordan法を使ったり、係数行列を与える際に再帰呼び出しをしたりとで結構コードが長くなってしまったのでここに残しておきます。

どういう手順？

  1. m個のデータをインプットします。ここでは良いデータが見つからなかったので適当な多項式に誤差項を乱数で与えました。
  2. 多項式とデータの残差の二乗の総和を、求める多項式の係数で偏微分します。これでn+1本の連立方程式が得られます。
  3. 連立方程式をときます。ここではよく知られたGauss-Jordan法を使いました。

もっとくやしく

まずコードを貼っておきます。

module subprog
   use globals
   implicit none
contains 
   subroutine gauss_jordan (a0,x,b,n)
      !部分pivot選択ありです
      integer,intent(IN) :: n
      real(8),intent(IN) :: a0(n,n),b(n)
      real(8),intent(OUT) :: x(n)
      integer i,j,m
      real(8) a(n,n+1),am,tmp(n+1),aji

      a(1:n,1:n)=a0
      
      do i=1,n
         a(i,n+1)=b(i)
      enddo

      do i=1,n
         m=i
         am=a(i,i)
         do j=i+1,n
            if(abs(am)<abs(a(j,i)))then
               am=a(j,i)
               m=j
            endif
         enddo

         if(am==0.0d0) stop "matrix A is not invertible!"
         if(i/=m)then
            tmp(1:n+1)=a(i,1:n+1)
            a(i,1:n+1)=a(m,1:n+1)
            a(m,1:n+1)=tmp(1:n+1)
         endif

         !消去開始
         a(i,i:n+1)=a(i,i:n+1)/am
         a(i,i)=1.0d0

         do j=1,n
            if(i==j)cycle
            aji=a(j,i)
            a(j,i:n+1)=a(j,i:n+1)-aji*a(i,i:n+1)
            a(j,i)=0.0d0
         enddo
      enddo

      do i=1,n
         x(i)=a(i,n+1)
      enddo
   end subroutine gauss_jordan

   subroutine mat_test(n,a,b)
      integer n
      real(8),intent(INOUT) ::a(n,n),b(n)
      call random_seed
      call random_number(a(1:n,1:n))
      call random_number(b(1:n))
   end subroutine mat_test

   function fun(x) result(y)
      real(8),intent(IN) :: x
      real(8) y
      y=0.1d0*x**3-0.2d0*x**2+0.9d0*x+1.0d0
   end function fun

   recursive subroutine set_vec(x,y,r,n,m,tmp,now)
   integer,intent(IN) :: n,m,now
   real(8),intent(IN) :: x(m),y(m)
   real(8),intent(INOUT) :: tmp(m),r(n+1)
   integer i
   real(8) :: sum=0.0d0
   
   if(now==0)then
      do i=1,m
      sum=sum+y(i)
      enddo
      r(now+1)=sum
      tmp(1:m)=1.0d0
   else
      call set_vec(x,y,r,n,m,tmp,now-1)
      do i=1,m
         tmp(i)=tmp(i)*x(i)
         sum=sum+y(i)*tmp(i)
      enddo
      r(now+1)=sum
   endif
   end subroutine set_vec

   recursive subroutine set_mat(x,y,c,n,m,tmp,now)
      integer,intent(IN) :: n,m,now
      real(8),intent(IN) :: x(m),y(m)
      real(8),intent(INOUT) :: c(n+1,n+1),tmp(m)
      integer i,j
      real(8) :: sum=0.0d0
      
      if(now==0)then
         c(1,1)=dble(m)
         tmp(1:m)=1.0d0
      else
         call set_mat(x,y,c,n,m,tmp,now-1)
         do i=1,m
            tmp(i)=tmp(i)*x(i)
            sum=sum+tmp(i)
         enddo
         if(now>n)then
            do j=0,2*n-now
               c(now-n+1+j,n+1-j)=sum
            enddo
         else
            do j=0,now
               c(1+j,now+1-j)=sum
            enddo
         endif
      endif
   end subroutine 

end module subprog

program main
   use globals
   use subprog
   implicit none
   integer :: m,i,j,n,fo=11,fi=12
   real(8) dx,x,er,sm
   real(8),ALLOCATABLE :: xi(:),yi(:),c(:,:),b(:),tmp(:),a(:)
   
   write(*,*)"input step m"
   read(*,*)m
   dx=20.0d0/dble(m)

   open(fo,file="output.d")
   do i=1,m
      x=-10.0d0+dble(i)*dx
      call random_seed
      call random_number(er)
      write(fo,*)x,fun(x)+50.0d0*er
   enddo
   close(fo)

   open(fi,file="output.d")
   allocate(xi(m),yi(m))
   write(*,*)"input dimention n"
   read(*,*)n
   do i=1,m
      read(fi,*)xi(i),yi(i)
   enddo
   close(fi)

   !ここから係数行列Aと初期条件のベクトルを構築していく
   allocate(c(n+1,n+1),b(n+1),tmp(m),a(n+1))
   call set_vec(xi,yi,b,n,m,tmp,n)
   call set_mat(xi,yi,c,n,m,tmp,2*n)
   deallocate(tmp,xi,yi)

   !Gauss-Jordan法で連立方程式を解き、出力
   call gauss_jordan(c,a,b,n+1)
   do i=0,n
      write(*,*)i,':',a(i)
   enddo

   open(fo,file="output2.d")
   do i=1,m
      x=-10.0d0+dble(i)*dx
      sm=0.0d0
      do j=1,n+1
         sm=sm+a(j)*x**(j-1)
      enddo
      write(fo,*)x,sm
   enddo

end program main

メインプログラムの最初のところではまずoutput.dに対して点列を与えています。ここでは区間[-10,10]をm等分してそれぞれをx_1,x_2,...,x_mとし、さらに適当な関数gを与えてy_i=g(x_i)+err(errは乱数による誤差項)とすることでm個の点列を得ました。

次は連立方程式を出してくるステップです。ここで、求める近似関数をf(x)とすれば、データとの残差の総和Rは

R=\sum_{i=1}^{m}\left(y_i-f(x_i)\right)^2

とかけます。ここではn次の多項式で近似することにしているのでf(x):=a_0+a_1x+a_2x^2+\cdots+a_nx^nとおけば

R=\sum_{i=1}^m\left(y_i-a_0-a_1x_i-a_2x_i^2-\cdots-a_nx_i^n\right)^2

と書くことができます。この式をa_k (k=0,1,\cdots,n)を独立変数とする関数だと見做すと、Rが最小となるとき\partial R/ \partial a_k=0となります。(それはそう)(a_kを横軸にとって下に凸な放物線を考えるとそれはそうだなって気分になってくる)
なのでRを素直にa_kで偏微分してやることで


\sum_{i=1}^m 2\left(y_i-a_0-a_1x_i-a_2x_i^2-\cdots-a_nx_i^n\right)(-x_i^k)=0 \\ \therefore~~\sum_{i=1}^m \sum_{j=0}^n a_jx_i^{k+j}=\sum_{i=1}^m y_ix_i^k~~~~\cdots\cdots(1)


を得ます。ここでベクトル\bm{b}=(b_k)~(k=0,1,\cdots,n)と(n+1)次正方行列C=(c_{k,j})~(k,j=0,1,\cdots,n)を

b_k:=\sum_{i=1}^my_ix_i^k \\ c_{k,j}:=\sum_{i=1}^mx_i^{k+j}

で定義すれば、先の(1)はn+1元連立方程式

C\bm{a}=\bm{b}

と同値になります。後はコレをGauss-Jordan法を用いて解くだけです。
Gauss-Jordan法とはなんぞやという話ですが、かっこいい名前が付いているもののやってることは普段連立方程式を解くときに使うのと同じアルゴリズムです。拡大係数行列を導入して左上から掃き出していきます。例えば3元1次連立方程式を解くときは下の図1のようになります。(tex打ちサボりました。)

f:id:jhonson1415:20200827153829p:plain
図1.掃き出し法で連立方程式を解く様子

更にここでは部分pivot選択というのをしています。掃き出し法では、ある行aを一つ選んで、その行aの定数倍を他の行bに足すことで他の行bの要素を消していますよね。実は、このとき絶対値が小さい行をaに選んでしまうと計算誤差が大きくなってしまいます。それを防ぐために、一度他の行を全部見てから、その中で最も絶対値が大きいものを選んでくるというのが部分pivot選択です。詳細は下の図2を参照です。図2では、有効数字4桁として5桁目を四捨五入して計算しました。

f:id:jhonson1415:20200827154120p:plain
図2.部分ピボット選択しなきゃいけない理由

また、コードの通り、係数行列Cとベクトル\bm{b}を与えるときには再帰subroutineを使っています。特に前者のsubroutineであるところのset_matの方では、(k+j)が一定となるような要素から埋めていくことで大幅に計算量を削減しています。

解析結果

g(x):=0.1x^3-0.2x^2+0.9x+1.0~~,m=300としたときの計算結果は以下のようになりました。上から順にn=3,10,100次の結果を図示しておきます。

f:id:jhonson1415:20200827155446p:plain
図3.n=3のときの解析結果
f:id:jhonson1415:20200827155516p:plain
図4.n=10のときの解析結果
f:id:jhonson1415:20200827155533p:plain
図5.n=100のときの解析結果

もともとの多項式が3次だったので、n=3のあたりではそこそこ精度がよかったのですが、n=6のときはなんか誤差がでっかくなっちゃってるのにも気づきました。n=7にすると落ち着いて来てました。最小二乗法完全理解マンがいたらコレの原因を教えてくれると嬉しいです。

f:id:jhonson1415:20200827155610p:plainf:id:jhonson1415:20200827155614p:plain
図6.n=6,7のときの解析結果

さいごに

　実際に解析で使えるようなプログラムを実装するのは楽しいですね。次はLaplace方程式の数値解法を実装して記事にできたら良いなと思ってます。また、Gauss-Jordan法は式の数が10万本くらいになると崩壊してくるので、別のアルゴリズムも実装していきたいですね。あと本当に最後に、まちカドまぞくの2期、本当に期待しています。明日辺り発狂する僕が見られると思います。

*1:一郎と読みます、ノートパソコンは次郎です

*2:第2版 数値計算のためのFortran90/95プログラミング入門、牛島省著、森北出版