球面調和関数変換を実装した話 - てれじょんのメモ帳

これはなに

　こんにちは、てれじょんです。ブログを書くのは久しぶりですね。最後に記事を書いてからというもの、FFTとか、FSTとかFCTとかまあ色々実装してはいた*1のですが記事を書くのが面倒(しかも別に書かなくてもググればだいたい情報が出てくるし、適当な教科書を読めば大丈夫)で、記事を書いていないのがかれこれ2年くらい続いていました(怠惰の言い訳か？)。しかし最近球面調和関数変換(以下SHT*2 )の実装をしたのですが、ググってもググっても自分で実装しましたみたいな話が全くなくて*3、不便だったので、自分が実装したまでの道筋を備忘録的に残しておこうと思って記事を書くことにしました。自分で実装してないライブラリを使いたくないというモノ好きの人はぜひ読んで下さい。あと何かいい記事を知っている人がいたら教えてください。

　記事の内容ですが、大半が石岡圭一『スペクトル法による数値計算入門』(東大出版会)に依っています。実装に最低限必要なことや、実装の時によくわからなかったことをメインで説明して、ググれば出てくるような数式とかの展開は端折っていこうと思っていますが、コレヤバいだろとか、もっとこういう説明のほうがわかりやすいだろってところがあったら教えてくれると嬉しいです。

SHT is 何

　球面上の関数 $g(\lambda,\mu)$ を球面調和関数 $Y_n^m$ で

$g(\lambda,\mu)=\sum_{n=0}^M\sum_{m=-n}^n s_n^mY_n^m(\lambda,\mu)$

のように展開して近似したい、というのがモチベーションです。ここに、 $\lambda$ は経度、 $\mu=\sin\phi$ はサイン緯度( $\phi$ が緯度)、 $M$ は切断波数です。

球面調和関数は、Legendre陪関数 $P_n^m(\mu)$ を用いて $Y_n^m(\lambda,\mu)=P_n^m(\mu)e^{im\lambda}$ と書くことができます。Legendre陪関数の取り方にはいくつか流儀がありますが、ここでは直交関係が簡単に書けるようにするために、

$P_n^m(\mu)=\sqrt{(2n+1)\frac{(n-|m|)!}{(n+|m|)!}}\frac{1}{2^n n!}(1-\mu)^{|m|/2}\frac{d^{n+|m|}}{d\mu^{n+|m|}}\left( (\mu^2-1)^n\right)$

と取ることにします。このように定義されたLegendre陪多項式には $\int_{-1}^1d\mu　P_n^mP_{n'}^m=2\delta_{n,n'}$ という直交関係があるので、球面調和関数には

$\int_{-1}^1d\mu\int_0^{2\pi}d\lambda ~Y_n^m(Y_{n'}^{m'})^*=4\pi \delta_{n,n'}\delta_{m,m'}$ という直交関係があることになります。

　この直交関係を用いれば、正変換が定義できます。逆変換の定義の両辺に $(Y_p^q)^*$ を掛けて球全体で積分することで

$s_p^q=\frac{1}{4\pi}\int_{0}^{2\pi}d\lambda\int_{-1}^1d\mu~ g(\lambda,\mu)Y_p^q(\lambda,\mu)$

$\therefore~~s_n^m=\frac{1}{4\pi}\int_{0}^{2\pi}d\lambda\int_{-1}^1d\mu~ g(\lambda,\mu)P_n^m(\mu)e^{im\lambda}$

を得ます。

　 $s_n^m$ の自由度について考えてみましょう。 $Y_n^m$ は $n\geq0,~-n\leq m\leq n$ で定義されており、 $Y_n^{-m}=(Y_n^{m})^*$ の関係があるので、 $g(\lambda,\mu)$ が球上の実関数であれば、 $s_n^{-m}=(s_n^m)^*$ を満たします。よって $s_n^m$ は $M\geq m \geq 0$ の成分のみ求めれば良く、また任意の $n$ に対して $s_n^0$ が実数であることがわかります。

　さて、以上のことを計算機上で実行するためには適当に離散化する必要があります。離散フーリエ変換の際には適当に等間隔に格子点を取れば積分を正確に評価できたのですが、今回緯度方向にはLegendre陪多項式で展開されているため、別の取り方が良さそうです。そこで、以下の公式を使います。

Gauss-Legendreの積分公式
- $\mu$ の $2J-1$ 次の多項式 $f(\mu)$ に対して、正確に $\int_{-1}^1f(\mu)d\mu=\sum_{k=1}^Jw_kf(\mu_k)$ である。
- ただし、 $\mu_k,~k=1,2,\dots,J$ はLegendre多項式 $P_J(\mu):=P_J^0(\mu)$ の $J$ 個の零点で、 $-1\lt\mu_1\lt\mu_2\lt\dots\lt\mu_n\lt1$
- また、 $w_k$ はGauss重みで、 $w_k:=\frac{2\sqrt{4J^2-1}}{JP_{J-1}(\mu_k){P_J}^{'}(\mu_k)}$

この公式を使うことによって、正変換の積分が正確に評価できます。すなわち、まず

$G^m(\mu):=\frac{1}{2\pi}\int_0^{2\pi}g(\lambda,\mu)e^{-im\lambda}d\lambda$

と置くと、この積分は経度方向に $K$ 個の等間隔の分点 $\lambda_k:=2\pi k/K,~~k=0,1,\dots,K-1$ を取って離散化すれば

$G^m(\mu)=\frac{1}{K}\sum_{k=0}^{K-1}g(\lambda_k,\mu)e^{-im\lambda_k}$

となります。これは(実)フーリエ正変換のルーチンを使うことで高速に計算できます。 $g(\lambda_k,\mu)$ を正変換すれば $m=0,1,\dots,K-1$ の $K$ 個の値が得られますが、 $m=0,1,\dots,M$ までしか使わないので、 $m=M+1,\dots,K-1$ の値は捨てましょう。(この時点では $\mu$ 方向には離散化されていませんが、これから見るように、 $\mu_j$ 上でのみ計算すればいいことがわかります。)

　このようにして得られる $G^m(\mu)$ を使えば、緯度方向の積分は

$s_n^m=\frac{1}{2}\int_{-1}^1 G^m(\mu)P_n^m(\mu)d\mu$

となりますが、Gauss-Legendreの積分公式より

$s_n^m=\frac{1}{2}\sum_{j=1}^J w_jG^m(\mu_j)P_n^m(\mu_j)$

と計算できます。以上のことをまとめれば、正変換は

$g(\lambda_k,\mu_j) \xrightarrow{FFT} G^m(\mu_j) \rightarrow s_n^m$

のように計算を回すことになります。

　逆変換はどうでしょうか。逆変換では、

$g(\lambda_k,\mu_j)=\sum_{n=0}^M\sum_{m=-n}^n s_n^m P_n^m(\mu_j)e^{im\lambda_k}$

を計算することになります。これもまずLegendre逆変換をしてからフーリエ逆変換を使うことを見越して、まず総和の順序を

$g(\lambda_k,\mu_j)=\sum_{m=-M}^M\sum_{n=|m|}^M s_n^m P_n^m(\mu_j)e^{im\lambda_k}$

のように入れ替えます。ただし、ここでは

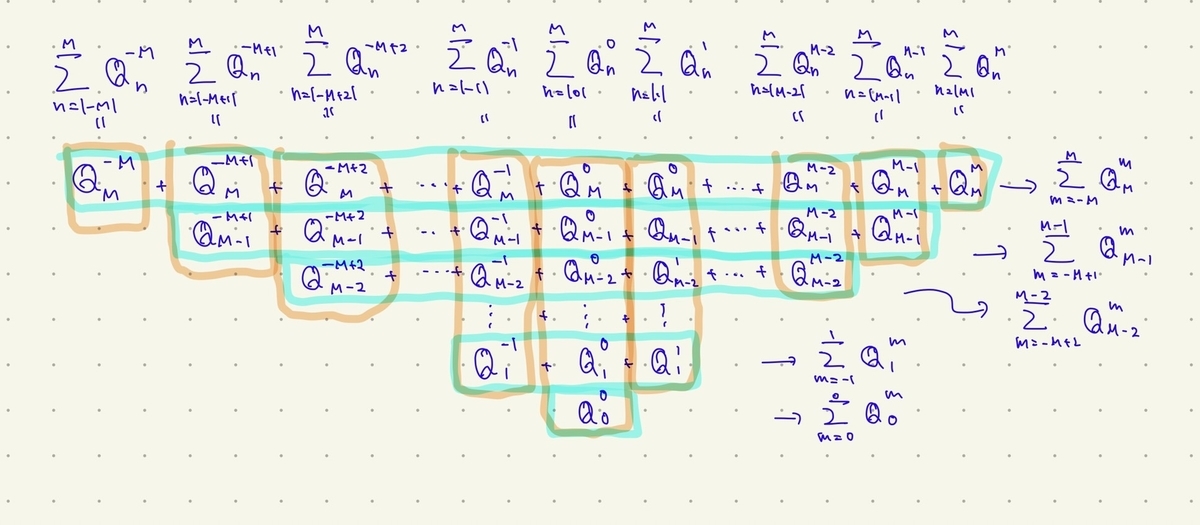
$\sum_{n=0}^M\sum_{m=-n}^n Q_n^m=\sum_{m=-M}^M\sum_{n=|m|}^M Q_n^m$

となることを使いました。あまり自明な感じがしませんが、これは図1のように全部書き下すと直感的に理解できます。先に横方向の和を取れば左辺に、先に方向の和を取れば右辺になります。

そして、 $m\geq0$ なる $m$ に対して $G^m(\mu)$ を

$G^m(\mu_j)=\sum_{n=|m|}^Ms_n^mP_n^m(\mu_j)$

と定義すれば、逆変換の式は

$g(\lambda_k,\mu_j)=\sum_{m=-M}^MG^m(\mu_j)e^{im\lambda_k}$

となりますが、これは切断波数 $M$ 、分点数 $K$ の(実)フーリエ逆変換となっていて、高速に計算できます。普通のFFTルーチンで計算できる形に変形してみましょう。まず $g(\lambda_k,\mu_j)$ は実数であることから、 $G^{-m}(\mu_j)=(G^m(\mu_j))^*$ がわかります。

さらに $e^{-im\lambda_k}=e^{im\lambda_{K-k}}$ であることから、負の波数を持つ成分を

$g(\lambda_k,\mu_j)=\sum_{m=0}^MG^m(\mu_j)e^{im\lambda_k}+\sum_{m=1}^MG^{-m}(\mu_j)e^{-im\lambda_k}$

$=\sum_{m=0}^MG^m(\mu_j)e^{im\lambda_k}+\sum_{m=1}^M(G^{m}(\mu_j))^*e^{im\lambda_{K-k}}$

$=\sum_{m=0}^MG^m(\mu_j)e^{im\lambda_k}+\sum_{m=K-M}^{K-1}(G^{K-m}(\mu_j))^*e^{im\lambda_{k}}$

のように正波数の領域に押し込めることができます。したがって、

$H^m(\mu_j)=G^m(\mu_j) ~(m=0,1,\dots,M)$

$H^m(\mu_j)=(G^{K-m}(\mu_j))~(m=K-M,K-M+1,\dots,K-1)$

$H^m(\mu_j)= 0~(otherwise)$

のように $H^m$ を定義すれば、

$g(\lambda_k,\mu_j)=\sum_{m=0}^{K-1}H^m(\mu_j)e^{im\lambda_k}$

と、普通の(実)フーリエ逆変換のルーチンで計算することができます。以上のことをまとめると、

$s_n^m\rightarrow G^m(\mu_j)(\rightarrow H^m(\mu_j))\xrightarrow{FFT^{-1}} g(\lambda_k,\mu_j)$

と計算を回すことになります。

実装するぜ

　実装しましょう。しかし変換を行う前に

Legendre多項式 $P_J(\mu)$ の $J$ 個の零点 $\mu_j$
Legendre陪多項式の値 $P_n^m(\mu_j),~(0\leq n\leq M,0\leq m\leq n)$

を予め求めておいたほうが効率が良さそうです*4。ですがLegendre陪多項式の定義式を思い出すと、 $n+|m|$ 階微分が含まれていて面倒です。また、零点を求めるときにNewton法を使うことにすれば、Legendre多項式の1階微分も必要になります。そこで必要になるのが以下の漸化式です。

$P_n^m=\sqrt{\frac{4n^2-1}{n^2-m^2}}\mu P_{n-1}^m-\sqrt{\frac{2n+1}{2n-3}}\sqrt{\frac{(n-1)^2-m^2}{n^2-m^2}}P_{n-2}^m~~\dots\dots(A)$
$(1-\mu^2)\frac{d}{d\mu}P_n=n\sqrt{\frac{2n+1}{2n-1}}P_{n-1}-n\mu　P_n~~\dots\dots(B)$

また、Legendre陪多項式の定義から、直ちに次のことがわかります。

$P_m^m=\frac{\sqrt{(2m+1)!}}{m!}\left(\frac{1-\mu^2}{4}\right)^{m/2}~~\dots\dots(C)$
$P_{m+1}^m=\mu\sqrt{2m+3}P_m^m(\mu)~~\dots\dots(D)$

　まず、零点の求め方を考えます。Newton法を使って零点を求めるとすれば、ある適当な初期推定値 $\mu_j^0=\cos\left(\frac{\pi(j-1/4)}{J+1/2}\right)$ *5から $P_J(\mu_j^0),~~P_J'(\mu_j^0)=\frac{d}{d\mu}P_J(\mu_j^0)$ を求め、更に漸化式

$\mu_j^{l+1}=\mu_j^l-\frac{P_J(\mu_j^{l})}{P_J'(\mu_j^{l})}$

を適当な回数回して、 $P_J(\mu_j^l)$ ないしは $|\mu_j^{l+1}-\mu_j^{l}|$ が十分小さくなったら反復を終える、という作業をします。ここではある与えられた $\mu$ に対して $P_J(\mu)$ を求める必要がありますが、それは漸化式(A)において $m=0$ とした式から再帰的に求められます。ただし、 $P_0(\mu)=1,~~P_1(\mu)=\sqrt{3}\mu$ を利用します。

再帰的にと言っているので(fortranなら)recursive属性のついた再帰関数を実装したくなるところですが、お察しの通りそれをやると計算量がえげつないことになるので、動的計画法チックに書いたほうが高速に計算できます。

$P_J(\mu)$ が求まってしまえば漸化式(B)から $P_J'(\mu)$ も求められるので、以上によって零点を求めることができました。適当な配列に突っ込んでおきましょう。

　各 $\mu_j$ 上のLegendre陪多項式の値 $P_n^m(\mu_j)$ の方はどうでしょうか。ここでは、まず対角成分 $P_m^m(\mu_j)$ とそのひとつ上の成分 $P_{m+1}^m$ をそれぞれ式(C),(D)によって求めて、それらの値から漸化式(A)を用いて上に登っていくという方針で求めます*6。図示すれば、図2.のようになります。

Legendre陪多項式をどのように配列に格納するか、という問題が残っています。 $n,~m$ については $0\leq m \leq M,~~m\leq n\leq M$ という範囲で定義されているので、全部で $J\sum_{k=0}^M k+1=J(M+1)(M+2)/2$ 個をしまうことになります。正変換と逆変換の式をグッと睨むと、 $j\gt n \gt m$ の順番に内側のループでたくさん呼び出されているので、それを考慮して格納したほうが良さそうです。ここでは $\verb#Ass_leg#(1:J,0:(M+2)(M+1)/2-1)$ と定義して、図3のようにしまいました。

$P_n^m(\mu_j)$ は $\verb#Ass_leg#(j,idx_m^n)$ に格納されることになります。ただし $idx_n^m:=\sum_{k=M-m+2}^{M+1}k+n-m+1-1$

$=m(2M-m+3)/2+n-m$ です。

　以上でLegendre陪多項式の構築ができたので、変換が実装できたことになります。やった～～

可視化、ベンチマーク結果

　さて、以上の変換を実装し、スペクトルデータからグリッドデータ(S2G, Spectrum to Gridなので)に変換した結果が図4.です。

ここでは、ある(n,m)にのみ $s_n^m$ を1にして、それ以外のスペクトル値を全部ゼロにして変換しました。こうすれば、球面調和関数の(実部の)値を得ることができます。量子力学の教科書などでよく見るような結果が得られているので、まあいい感じなんじゃないんでしょうか。

ちなみに可視化にはParaviewを使いました。ググれば使い方が出てくる程度の使い方しかしていません。でもそのうちParaviewを使って二次元球面上の実験結果の可視化みたいなことをやろうも思っていて、もしそれができたらParaviewのことも記事にしたいとは思ってます*7。

　さて、計算時間の方はどうでしょうか。教授から借りてるノートパソコンでベンチマークしました。スペックはCPU:i7-2640M, メモリ:8GBです。世界最速のSHTライブラリであるところのispack*8との比較結果を以下に示します。表中の値は計算時間[sec]です。

切断波数	M=511	M=1023	M=2047
telibrary*9 bwd	0.599	4.69	-
ispack bwd	0.019	0.0579	0.392
telibrary fwd	0.731	5.65	-
ispack fwd	0.0093	0.0469	0.356

惨敗で草

ispackより2桁、ひどいときで3桁くらい遅いです。私のライブラリではM=2047のときはもはや計算が不可能でした。 $P_n^m(\mu_j)$ を素直に求めて素直にメモリに突っ込むように実装したので、切断波数がデカいとメモリに乗らなくなるのが原因です。M=2047だと、Legendre陪多項式だけでだいたい8*2048*2049*2050/2[bytes]≒34.4[GB]の記憶容量が必要になります。正気か？

高速化に向けて

　前節で見たように、素人が見様見真似で実装しただけではカスみたいな遅さのプログラムが出来上がることがわかりました。FFTの場合は適当に実装してもまあまあな速度が出るのでフルスクラッチの数値計算スキームを作ることができたのですが、SHTはなかなか一筋縄ではいかなそうです。

　このままだと悔しいので当然高速化していきたい訳ですが、どういう方向があるのか？という話を最後にちょっとだけしたいと思います。

　今回の実装では並列処理を全く挟んでいない、単純極まりないコードを書きました。普段使うような計算機では、OpenMPなどを使えばあまり複雑なことを考えずに並列計算をすることができるので、そうすれば定数倍程度は速くなりそうです。

　また、前節で見たように、Legendre陪多項式を予め求めてしまうとクソデカ配列になってしまい、キャッシュどころかメモリにも載らなくなってしまう、という問題点があります。これに関しては、変換するごとにLegendre陪多項式の値を求めることで解決できるらしいです。詳しくは注釈で紹介した論文をご覧ください。また、「球面調和関数変換　キャッシュ」などで検索すると、ispack製作者であるところの石岡圭一氏のスライドが色々出てきます。この論文ではテクニカルな漸化式と命令を用いてLegendre陪多項式の計算量を通常の1/3程度に抑えていますが、そこまでしなくてもうまいことやったらまあまあ速くなるような気がします。

　また、ナイーブな手法としては、ガウス緯度の偶奇性を利用してjについての和を半分にするという手法もあるようです。いずれにせよ、できることはまだまだありそうです。

まとめ

クソ遅いSHTライブラリを構築した
悔しい
SHT(Sugoku Hayai Transform)にしたい
そうでなくてもせめて卒業研究で使える程度の速さにはしたいので、修行を積みます

*1:例えばこういうのを実装していました。対流不安定な成層上でベナール対流が発達する様子です。上が温度場、下が流線関数を描いています。

鉛直方向は境界条件の問題からフーリエ級数じゃなくサイン級数で展開する必要があり、そのためにFSTとFCTを実装しました。

*2:Spherical Harmonic Transformの略。HTTみたいですね。

*3:てかこの令和の時代に自分でSHTのライブラリを作りたいなんて人がそもそもいないんでしょうね。どのライブラリもゴリゴリにチューンされてて勝ち目なんてないし。

*4:ただ、高速化の観点から見ると、Legendre陪多項式の値は全部求めるとクソでかい配列になって、キャッシュに乗らなくなってしまうので、変換のたびに求めたほうが効率がいいらしいです。詳しくはIshioka, K. (2018). A new recurrence formula for efficient computation of spherical harmonic transform. In Journal of the Meteorological Society of Japan (Vol. 96, Issue 2, pp. 241–249). Meteorological Society of Japan. https://doi.org/10.2151/jmsj.2018-019 を読んでください。

*5:なんかこういう初期値を取るといい感じに求めることができるっぽいです

*6: $P_n^m$ の上付き添字を動かす漸化式をどっかから引っ張ってきて、 $P_n$ の値から $P_n^m$ を求めようとしたこともあったのですが、それをすると計算誤差がデカくなるので、上の手法を採用しました。